[1]姜聪颖,侯成敏*.一类非线性奇异分数阶微分方程解的存在唯一性[J].延边大学学报(自然科学版),2020,46(04):283-288.
　JIANG Congying,HOU Chengmin*.Existence and uniqueness of solutions for a class of nonlinear singular fractional differential equations[J].Journal of Yanbian University,2020,46(04):283-288.
点击复制

一类非线性奇异分数阶微分方程解的存在唯一性

《延边大学学报(自然科学版)》[ISSN:1004-4353/CN:22-1191/N] 卷: 第46卷 期数: 2020年04期 页码: 283-288 栏目: 基础科学研究 出版日期: 2020-12-20
Title:
Existence and uniqueness of solutions for a class of nonlinear singular fractional differential equations
文章编号:
1004-4353(2020)04-0283-06
作者:
姜聪颖;  侯成敏*
( 延边大学 理学院, 吉林 延吉 133002 )
Author(s):
JIANG Congying;  HOU Chengmin*
( College of Science, Yanbian University, Yanji 133002, China )
关键词:
边值问题;  奇异分数阶微分方程;  Caputo分数阶导数;  Banach不动点定理;  Schauder不动点定理
Keywords:
boundary value problem;  singular fractional differential equation;  Caputo fractional derivative;  Banach fixed point theorem;  Schauder fixed point theorem
分类号:
O175.6
文献标志码:
A
摘要:
研究了一类非线性奇异分数阶微分方程的边值问题: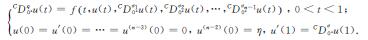首先利用Banach不动点定理和Schauder不动点定理得到了此类非线性分数阶微分方程解的存在性和唯一性的相关结论和定理,然后利用两个实例验证了文中所得的主要结论.
Abstract:
We study a class of boundary value problems of nonlinear singular fractional differential equations: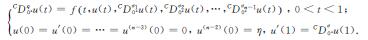Firstly, Banach fixed point theorem and Schauder fixed point theorem are used to obtain relevant conclusions and theorems about the existence and uniqueness of solutions of such nonlinear fractional differential equations, and then the main conclusions obtained in this paper are verified by two examples.

参考文献/References:

[1] AGARWAL R P, O’REGAN D, STANEK S. Positive solutions for dirichlet problem of singular nonlinear fractional differential equation[J]. Electron J Math Anal, 2011,371:57-68.
[2] YAN R, SUN S, LU H, et al. Existence of solutions for fractional differential equations with integral boundary conditions[J]. Adv Differ Equ, 2014(1):1-13.
[3] GUEZANE -LAKOUD A, BENSEBAA S. Solvability of a fractional boundary value problem with fractional derivative condition[J]. Arab J Math, 2014,3:39-48.
[4] KILBAS A A A, SRIVASTAVA H M, TRUJILLO J J. Theory and applications of fractional differential equations[J]. Elsevier Amsterdam, 2006,204:91-99.
[5] 葛琦,侯成敏.一类分数阶差分方程边值问题递增正解的存在性[J].吉林大学学报(理学版),2013,51(1):47-52.
[6] 刘欢.带P-拉普拉斯算子的delta -nabla分数阶差分边值问题正解的存在性[D].延吉:延边大学,2017.
[7] LI R G. Existence of solutions for nonlinear singular fractional differential equations with fractional derivative condition[J]. Department of Mathematics, 2014,214(1):1-12.

相似文献/References:

[1]孙明哲,韩筱爽.一类分数阶q-差分边值问题的正解[J].延边大学学报(自然科学版),2013,39(04):252.

备注/Memo

收稿日期: 2020-08-30 基金项目: 吉林省教育厅“十三五”科学技术研究项目(JJKH20170454KJ)
*通信作者: 侯成敏(1963—),女,教授,研究方向为微分方程及其应用.

更新日期/Last Update: 2020-12-20